 Calculation of water productivity
Calculation of water productivity
Water resources to support rainfed and irrigated agriculture also are under pressure, making the efficiency with which water is converted to food, water productivity (WP), another critical benchmark for food production and resource use efficiency (French and Schultz, 1984, Bessembinder et al., 2005; Passioura, 2006).
The full water balance can be defined as (see table 1 and Fig 1 beside for definition of variables):
I + P + C + Rin + Lin + S1 = E + T + D + Rout + Lout + S2
Lateral flows (L), surface run-on (Rin), and capillary rise (C) can be important components of the water balance in specific cropping systems and regions, however, current simulation models do not have the level of sophistication or data inputs are not available for robust estimation of these components. Hence, the above equation should be simplified as follows:
I + P + S1 = E + T + D + Rout + S2
To a large degree, water losses through drainage (D) and surface runoff (Rout) are unavoidable, therefore, these should be subtracted from the water inputs to calculate the amount of water that is actually available for the crop during the growing season. Likewise, some of the water available during the growing season remains unused in the soil profile by the time of physiological maturity. Hence, we defined crop water availability (CWA) as the amount of water supply during the crop growing season (from available soil water at sowing (S1), precipitation (P), and also irrigation (I) in irrigated systems) after discounting unavoidable losses through surface runoff, deep drainage and the residual available soil water left in the soil profile at crop physiological maturity (S2). The above equation can be re-written as follows, in which ET represents evapotranspiration:
I + P + S1 - D - Rout - S2 = ET
Crop models simulate crop growth and development under potential or water-limited conditions with no nutrient deficiencies and incidence of pathogens, insect pests, and weeds. The simulated ET by crop models represents the CWA for a crop that received optimal management and maximize the amount of transpired water in relation to the other water losses. Hence, potential (WP-potential) and actual water productivity (WP-actual) can be calculated as follows:
WP-potential (kg ha-1 mm-1) = Yp / CWA (irrigated crop systems)
WP-potential (kg ha-1 mm-1) = Yw / CWA (rainfed or partially-irrigated crop systems)
WP-actual (kg ha-1 mm-1) = Ya / CWA
where Yp is the simulated yield potential (kg ha-1), Yw is the simulated water-limited yield potential (kg ha-1), Ya is the actual yield (kg ha-1), and CWA is the crop water availability (mm) which is estimated from the simulated ET.
References:
Passioura, J., 2006. Increasing crop productivity when water is scarce—from breeding to field management. Agric. Water Management 80, 176–196.
Bessembinder, J.J.E., Leffelaar, P.A., Dhindwal, A.S., Ponsioen, T.C., 2005. Which crop and which drop, and the scope for improvement of water productivity. Agric. Water Manage. 73, 113–130.
French, R.J., Schultz, J.E., 1984. Water use efficiency of wheat in a Mediterranean type environment. I. The relation between yield, water use and climate. Aust. J. Agric. Res. 35, 743–764.
Table 1 Variables for water balance calculations (all in mm)
|
* sum over the period from sowing to physiological maturity
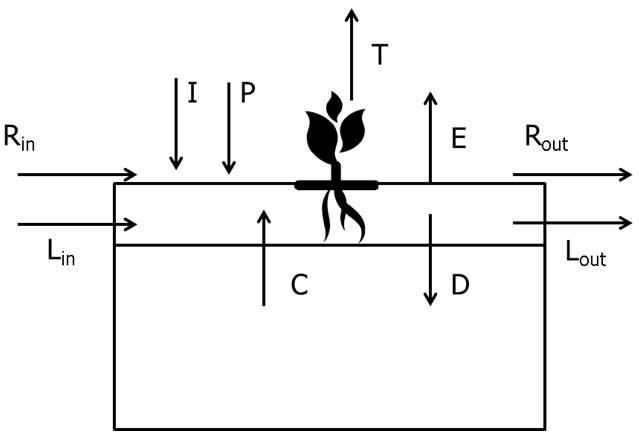
Figure 1. Field level water balance
